CSS Transform

September 23, 2014

本文翻译自：http://desandro.github.io/3dtransforms/

知识点

  • perspective-origin默认在50%，50%
  • transform不影响文档流
  • 多次transform函数作用时，后一次变换的坐标系为上一次变换完毕后的坐标系

Perspective 视点

To activate 3D space, an element needs perspective. This can be applied in two ways: using the transform property, with the perspective as a functional notation. 首先为了激活3D空间，需要给元素加上视点（perspective），有两种形式：用transform属性，然后把perspective当做一个函数

transform: perspective( 600px );

或者直接使用perspective属性：

perspective: 600px;

Perspective property at work

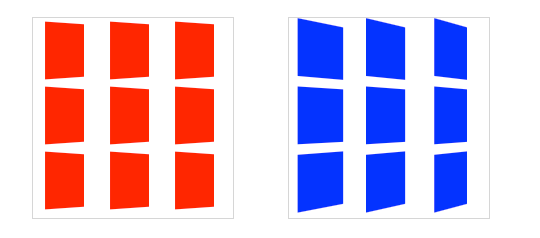
两种形式都会激活一个3D空间,但是他们是有差别的.函数符号可以直接给单个元素应用3D变换。比如上面例子左侧的。但是当用在多个元素上时，他们并不会作用在一起，而是分别对每个元素应用，这样看起来就不是我们预期的，比如下图的例子。这种情况下，我们需要使用perspective到他们的父元素上,这样每个子元素就会共用这个视点。他们看起来就像是一个统一的3D系统。

Perspective differences when used with child elements

perspective的值决定3D效果的强度。你可以把它想象成与目标物体的距离，它的值越大,你离目标越远,反之亦然。perspective: 2000px;会产生一个微弱的3D效果，就想我们在很远的地方拿望远镜来看的，perspective: 100px;产生一个强烈的3D效果，就想近距离观察一个很大的物体。

3D空间的变换点(消失点)默认是在物体的中央，你可以通过perspective-origin来改变这个位置:

perspective-origin: 25% 75%;

Intense perspective value, with vanishing point modified

3D变换函数

3D变换和2D用同一个属性：transform，如果你对2D变换比较熟的话，那3D你看起来也不会太陌生:

  • rotateX( angle )
  • rotateY( angle )
  • rotateZ( angle )
  • translateZ( tz )
  • scaleZ( sz )

与translateX在X轴上平移元素类似，translateZ在Z轴上平移元素，Z轴方向是这样的：屏幕背后是负的，屏幕前面是正的，距离屏幕越远，数值越大。

rotate函数可以使元素在相应的轴上旋转。这个和直觉有点不一样.用rotateX( 45deg )会使顶边向后移，底边向前移。

CSS 3D transform functions

还有三个简写的方式：

  • translate3d( tx, ty, tz )
  • scale3d( sx, sy, sz )
  • rotate3d( rx, ry, rz, angle )

These foo3d() transform functions also have the benefit of triggering hardware acceleration in Safari. Dean Jackson, CSS 3D transform spec author and main WebKit dude, writes

实质上，任意的有3d操作的的函数都会触发硬件加速，即使它只做了2d变换，或者啥也没干。注意这只是目前的行为，未来可能会改变（所以我们没有记录下来，也没有鼓励这么做）。但在某些情况下这是很有用的，可以显著提升渲染性能。

为了简单期间，这些demo只用了最基本的transform函数，但如果要用到生产环境下，确保用的是foo3d（）函数来获取最佳的性能。

Matrix 简要解释

假设每一个列是一个点向量，前三行的最后一个数决定平移的量，最后一行的前三个元素不是用来做变换位置的，他们是用来做视点的投影用的。If (as your question suggests) the convention is that points are column vectors, and the last elements of the first 3 rows determine the translation, then the first 3 elements of the bottom row are not a positional offset: the 4th row of a transformation matrix is used for perspective projection, which is how the camera maps 3D points onto the 2D viewport. A sketch of how the 4x4 matrix is used to map points:

result   =       4x4 matrix      *  point

[ x' ]       [ Rxx Rxy Rxz Tx ]     [ x ]
                                                    R** is the rotation/scaling matrix
[ y' ]       [ Ryx Ryy Ryz Ty ]     [ y ]
         =                       *             ->   T* is the translation vector
[ z' ]       [ Rzx Rzy Rzz Tz ]     [ z ]
                                                    P* fixes the camera projection plane
[ w' ]       [ Px  Py  Pz  Pw ]     [ w ]

-> x' = dot_product3([Rxx,Rxy,Rxz], [x,y,z])  + Tx * w
-> y' = dot_product3([Ryx,Ryy,Ryz], [x,y,z])  + Ty * w
-> z' = dot_product3([Rzx,Rzy,Rzz], [x,y,z])  + Tz * w
-> w' = dot_product4([Px,Py,Pz,Pw], [x,y,z,w])

Demo time

Card Flip

1
2

  • tab1
  • tab2
  • tab3
This is a panel
This is a panel
This is a panel